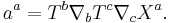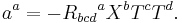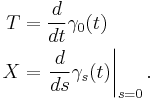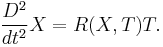Geodesic deviation equation
In general relativity, the geodesic deviation equation is an equation involving the Riemann curvature tensor, which measures the change in separation of neighbouring geodesics or, equivalently, the tidal force experienced by a rigid body moving along a geodesic. In the language of mechanics it measures the rate of relative acceleration of two particles moving forward on neighbouring geodesics. In differential geometry, the geodesic deviation equation is more commonly known as the Jacobi equation.
Let T a be the tangent vector to a given geodesic γ, and X a a vector field along γ connecting it to an infinitesimally near geodesic (the deviation vector). The relative acceleration of the infinitesimally near geodesic is defined by
The geodesic deviation equation asserts that
To more rigorously formulate the equation, let γs(t) be a 1-parameter variation through geodesics: i.e., for each fixed s, the curve swept out by γs(t) as t varies is a geodesic with affine parameter. The tangent vector and deviation vector are respectively defined by
In order that γs be a variation through geodesics, a necessary condition is that the geodesic equation holds:
The geodesic deviation equation can be derived from the second variation of the point particle Lagrangian along geodesics, or from the first variation of a combined Lagrangian. The Lagrangian approach has two advantages. First it allows various formal approaches of quantization to be applied to the geodesic deviation system. Second it allows deviation to be formulated for much more general objects than geodesics (any dynamical system which has a one spacetime indexed momentum appears to have a corresponding generalization of geodesic deviation).
See also
References
- Stephani, Hans (1982), General relativity - an introduction to the theory of the gravitation field, Cambridge University Press, ISBN 0-521-37066-3.
- Wald, Robert M. (1984), General Relativity, ISBN 978-0-226-87033-5.